TopOp

Phase field topology optimization for a simple cantilever subject to a concentrated load on the right hand side. This primarily tests the Integrator::TopOp integrator, but also tests the static mechanics capability as well as BC::Expression.

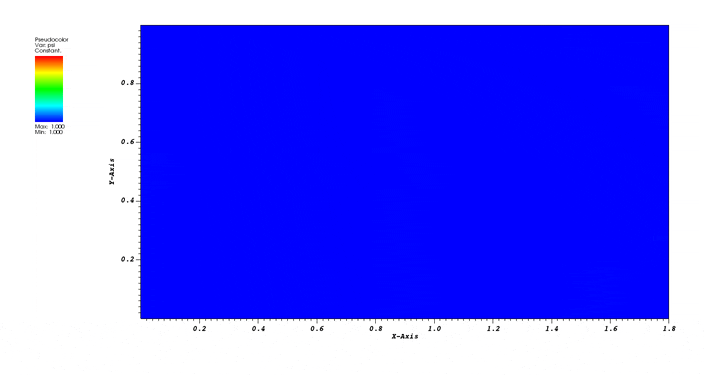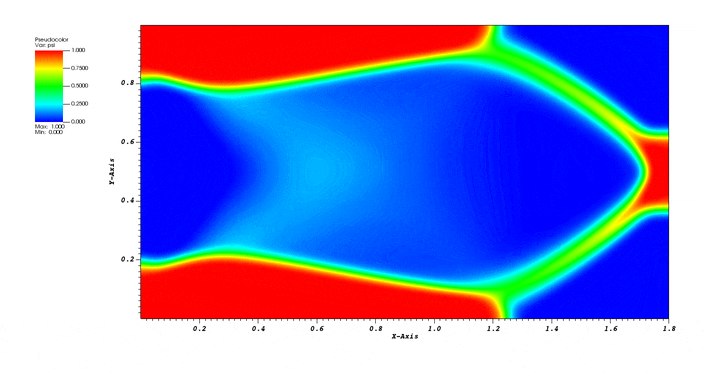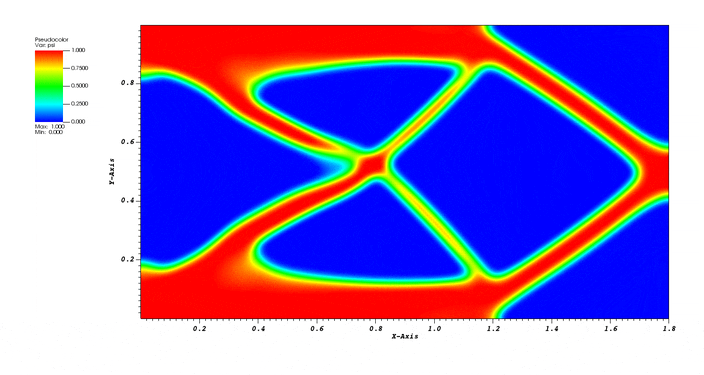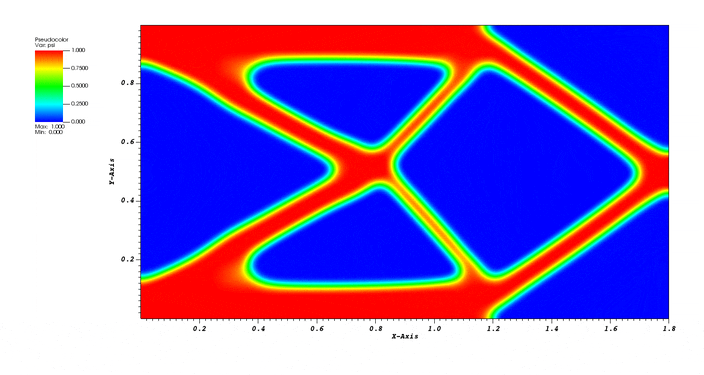
The following publication documents the method in more detail.

Vinamra Agrawal and Brandon Runnels. Robust, strong form mechanics on an adaptive structured grid: efficiently solving variable-geometry near-singular problems with diffuse interfaces. Computational Mechanics, 2023.

serial

	Two-dimensional
	Serial
	Not validated
	11.30s (waldorf)
	./bin/topop-2d-g++ tests/TopOp/input stop_time="1.0"

parallel

	Two-dimensional
	Parallel (4 procs)
	Validated using check script
	mpiexec -np 4 ./bin/topop-2d-g++ tests/TopOp/input stop_time="10.0"

coverage

	Two-dimensional
	Serial
	Not validated
	./bin/topop-2d-g++ tests/TopOp/input stop_time="0.2" solver.fixed_iter="10"

Input file (../../tests/TopOp/input)

#@ 
#@ [serial]
#@ exe = topop
#@ dim = 2
#@ args=stop_time=1.0
#@ check=false
#@ benchmark-waldorf = 11.30
#@
#@ [parallel]
#@ exe = topop
#@ dim = 2
#@ nprocs = 4
#@ args=stop_time=10.0
#@ check=true
#@ 
#@ [coverage]
#@ exe = topop
#@ dim = 2
#@ args=stop_time=0.2
#@ args=solver.fixed_iter=10
#@ check=false
#@ coverage=true
#@
alamo.program               = topop
plot_file		    = tests/TopOp/output

timestep		    = 0.1
stop_time		    = 20.0

# amr parameters
amr.plot_int		    = 1 #10000
amr.max_level		    = 2
amr.n_cell		    = 64 32 32
amr.blocking_factor	    = 4
amr.regrid_int		    = 1
amr.grid_eff		    = 1.0
amr.node.all = 1
amr.thermo.plot_dt = 0.1

# geometry
geometry.prob_lo	    = 0 0 0
geometry.prob_hi	    = 1.8 1 1
geometry.is_periodic	    = 0 0 0

#
# Isotropic elastic model
#
model.E = 3.70 
model.nu = 0.22

#
# Topology optimization parameters
#
alpha = 200.
beta = 0.05 
gamma = 50000.0
L.str = 0.005 
volume0 = 0.5
lambda.str = 400.0

#
# BCs for psi variable
#
psi.ic.type = constant
psi.ic.constant.value = 1.0
psi.bc.type.xhi = NEUMANN
psi.bc.type.xlo = NEUMANN
psi.bc.type.yhi = NEUMANN
psi.bc.type.ylo = NEUMANN


#### Canonical test case: cantilever with load at tip
bc.type = expression
bc.expression.type.xloylo = disp disp
bc.expression.type.xlo    = disp disp
bc.expression.type.xloyhi = disp disp
bc.expression.type.ylo    = trac trac
bc.expression.type.yhi    = trac trac
bc.expression.type.xhi    = trac trac
bc.expression.type.xhiylo = trac trac
bc.expression.type.xhiyhi = trac trac
bc.expression.val.yhi = "0.0" "0.0" 
bc.expression.val.xhiylo = "0.0" "0.0"
bc.expression.val.xhiyhi = "0.0" "0.0"
bc.expression.val.ylo = "0.0" "0" 
bc.expression.val.xhi = "0.0" "-0.1 * (y > 0.45) * (y < 0.55)" 
#L.str = 0.01

#
# Solver inputs
#
elasticop.small=0.01
solver.bottom_solver = smoother
solver.tol_abs = 1E-16 # This is very important for near-singular problems!!!
solver.verbose = 3
solver.nriters = 1
solver.fixed_iter=2000

#
# Mechanics inputs
#
interval = 1
print_residual=1
eta_ref_threshold = 0.05
elastic_ref_threshold = 100000
zero_out_displacement = 1