ThermoElastic

This test demonstrates multiphysics coupling using the ThermoElastic integrator that inherits both from HeatConduction and Mechanics. In the test, the domain is initially stress-free and at T=0. Thermal evolution is driven by the lower and left boundaries that are at T=1. The circular inclusion has a coefficient of thermal expansion, while the matrix does not. So, as the inclusion heats up, it expands, inducing a stress distribution.

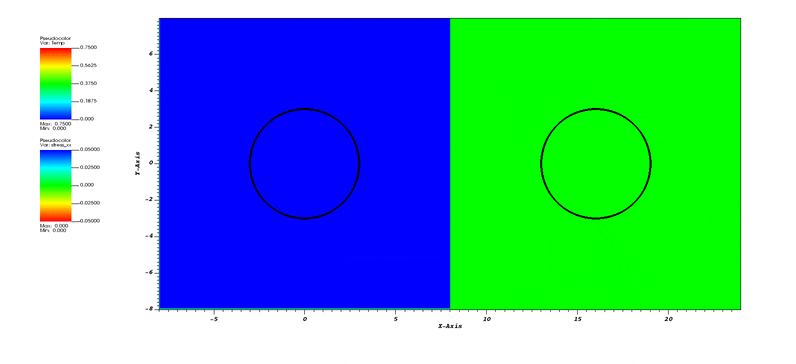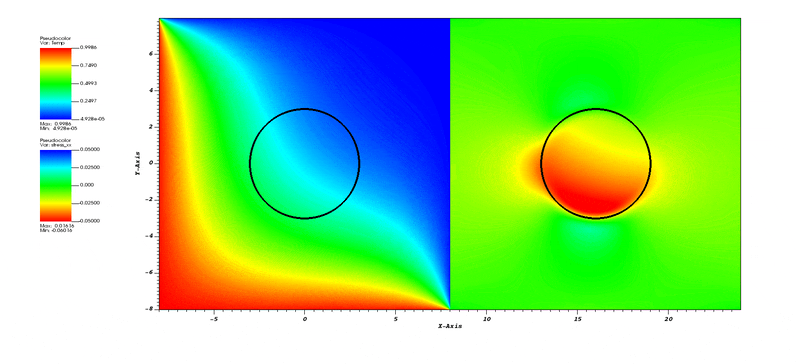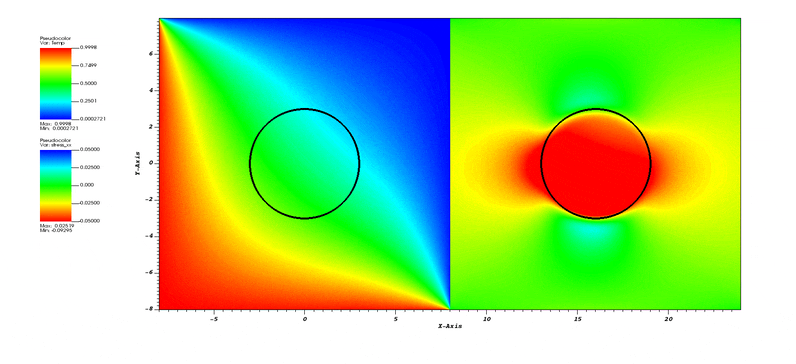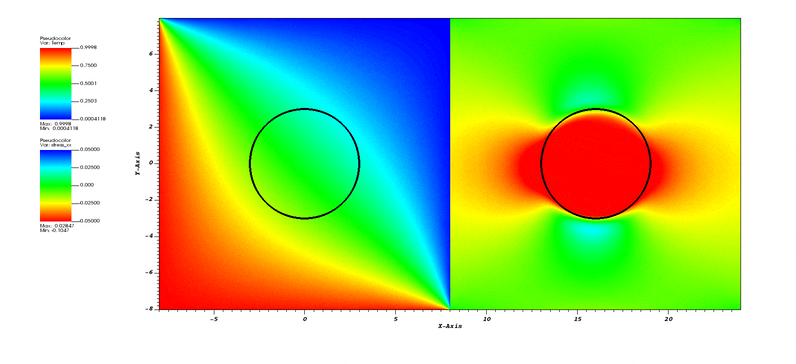
2d

	Two-dimensional
	Serial
	Validated using check script
	./bin/thermoelastic-2d-g++ tests/ThermoElastic/input stop_time="10"

2d-coverage

	Two-dimensional
	Serial
	Not validated
	./bin/thermoelastic-2d-g++ tests/ThermoElastic/input stop_time="1"

Input file (../../tests/ThermoElastic/input)

#@
#@ [2d]
#@ dim=2
#@ check=true
#@ exe=thermoelastic
#@ args=stop_time=10
#@ 
#@ [2d-coverage]
#@ dim=2
#@ check=false
#@ exe=thermoelastic
#@ args=stop_time=1
#@ coverage=true
#@

alamo.program = thermoelastic

plot_file     = tests/ThermoElastic/output

# Simulation length
timestep = 0.005
stop_time = 40.0

# amr parameters
amr.plot_int		    = 100
amr.max_level		    = 3
amr.n_cell		    = 32 32 32
amr.blocking_factor	    = 4
amr.regrid_int		    = 50
amr.grid_eff		    = 1.0

amr.cell.all = 1

# geometry
geometry.prob_lo	    = -8 -8 -8 
geometry.prob_hi	    = 8 8 8
geometry.is_periodic	    = 0 0 0


alpha = 0.001 0.0


#
# HEAT TRANSFER MODEL
#

hc.heat.alpha = 1.0
hc.heat.refinement_threshold = 0.1

# Specify initial conditions
hc.ic.type = sphere
hc.ic.sphere.center = 0.5 0.5 0.5
hc.ic.sphere.radius = 0.25
hc.ic.sphere.inside = 0.0

# Boundary conditions
hc.bc.temp.constant.type.xhi = dirichlet
hc.bc.temp.constant.type.xlo = dirichlet
hc.bc.temp.constant.type.yhi = dirichlet
hc.bc.temp.constant.type.ylo = dirichlet
hc.bc.temp.constant.type.zhi = dirichlet
hc.bc.temp.constant.type.zlo = dirichlet
hc.bc.temp.constant.val.xhi  = 0.0
hc.bc.temp.constant.val.xlo  = 1.0
hc.bc.temp.constant.val.yhi  = 0.0
hc.bc.temp.constant.val.ylo  = 1.0
hc.bc.temp.constant.val.zhi  = 0.0
hc.bc.temp.constant.val.zlo  = 1.0

#
# ELASTICITY MODEL
#

el.interval = 100

# ellipse configuration
el.ic.type        = ellipse
el.ic.ellipse.a   = 3.0 3.0 3.0  # ellipse radii
el.ic.ellipse.x0  = 0 0 0 # location of ellipse center
el.ic.ellipse.eps = 0.8 # diffuse boundary

el.bc.type = constant

# elastic moduli
el.nmodels = 2
el.model1.E = 210 
el.model1.nu = 0.3
el.model1.F0  = 0 0 0 0 0 0 0 0 0 # eigenstrain
el.model2.E = 210 
el.model2.nu = 0.3
el.model2.F0  = 0 0 0 0 0 0 0 0 0 # eigenstrain
el.solver.verbose = 4
el.solver.nriters = 1

el.ref_threshold = 5E-5
el.eta_ref_threshold = 5E-5